Physics Notes: The Standard Model

Lecture 8: Mar 1, 2010 Back to PHY30

Review of Spontaneous Symmetry Breaking

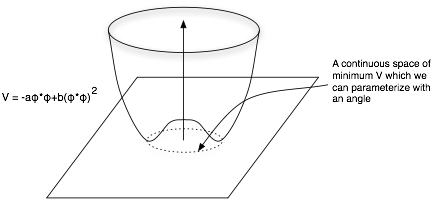
A field gradient along costs energy.

There was a question about starting the field everywhere at 0 (on top of the peak in the center). With any kind of jostling, the field value with respect to space would initially break up into a set of domains as the field value would rapidly evolve toward a point on the V minimum curve. Then the domains would bleed into each other to minimize energy. [Some kind of energy dissipation must also be involved or you would maintain high levels of oscillation]

Discrete cases

One could imagine potential functions that have a specific number of equivalent minima arranged evenly along the unit circle in our field value space. Such a rotation symmetry would be known as a Z(n) symmetry. This kind of symmetry would yield domain walls if you fixed the left and right edges of an area at two different values. The domains would have nearly constant with rapid change of at domain boundaries. The Z(4) case might look like this:

In our first figure, there is a potential energy symmetry with respect to . Across space we can have arbitrarily slow variation in , meaning that we can have arbitrarily low energy (Goldstone boson). If energy goes to 0 with 0 momentum, then the quanta is massless.

In our more complex potential function there are also two directions, but one has mass and the other doesn’t. Oscillations along have mass.

In this and in our more complex , there is a conserved quantity associated with our direction symmetry. It is similar to angular momentum in that it is quantized and associated with a rotation (even though the rotation is in the field value instead of in 3 space). The answer is “charge”.

Note: Real photons don’t have a mass. But, photons in a superconductor do acquire a mass. The 0 momentum state still has energy.

See: http://www.search.com/reference/Higgs_mechanism and search for superconductivity.

Response to question about massive vs. mass-less particles

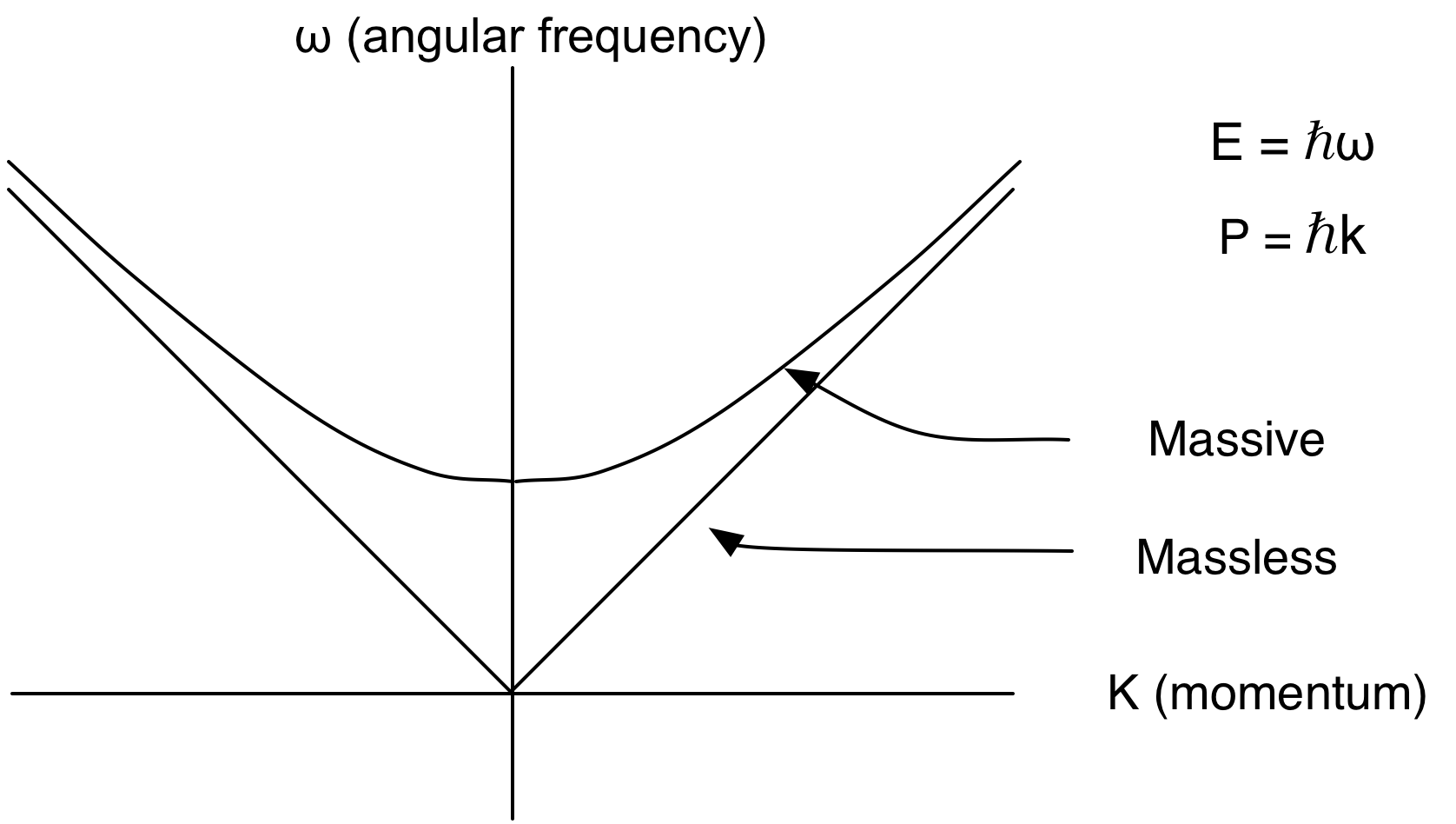
The Higgs Field

“The Goldstone boson is eaten by the gauge boson, giving mass to the gauge boson via the Higgs field” [I am pretty sure I have the quote slightly wrong, but I think the meaning is ok]

There is a collection of particles in the standard model that must have symmetry breaking to get masses.

Are there particles that don’t need symmetry breaking to get masses? Yes, but the mass is too large to observe. We do know that there are more particles – dark matter for instance.

Gauge bosons need symmetry breaking to get their mass.

Take a complex field with our potential function that has a minimum at .

Our Lagragian:

If we had written our Lagrangian in terms of , then we would have two fields each of which would have mass. In terms of the part will have mass and will not.

Now let . This where is the position of the minimum of V. now represents a small distance from that minimum and there will be oscillation about h=0. [I take it that h – Higgs] These oscillations would be the very massive particles that were described earlier. For low energy behavior it is as if is frozen at . Our Lagrangian would then simplify to:

Apply a transformation

If is a constant, then this transformation preserves the Lagrangian. If it is not a constant, then we have to compensate for the terms that will pop up. Doing this requires introduction of the vector potential and a covariant form of the derivative.

(Transform of A. E and B derived from A)

(Definition of field tensor)

Our Lagrangian becomes:

[See lecture 7 notes for review of how this version of the Lagrangian is invariant with respect to our variable angle transform.]

Now suppose that our ground state symmetry is broken and we have preferred . Then we would have a Goldstone boson and a photon, both of which are massless. To have a mass we would need to add a term like . We can’t do that directly without breaking our Lagrangian.

[I am trying to get all the upper/lower indices correct here based on my sketchy notes. This may not follow the lecture path completely, but ends up at the same place]

Lets look closer at the term under the assumption that .

Now substituting

That last term looks like the mass term that we couldn’t add just by itself. Our total Lagrangian now looks like:

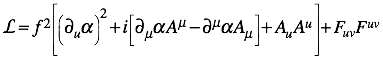
[The middle term is interesting because the difference between lower and upper A is the time component and there is no difference for – it doesn’t really matter because all terms are about to go away]

Now let’s make the substitution that . We can do this because our Lagrangian does not change under this transform. This change will kill off the dependency because the new will just be a constant. We end up with

Our Goldstone boson has been “eaten” and we have a mass term for our boson. The mass depends on the location f of the minimum of .

Some additional reading on the topic:

http://en.wikipedia.org/wiki/Gauge_theory#Gauge_fields

[An interesting question here would be what would happen if had multiple minimums. It seems to me that the result would be a family of particles that differed only in their mass, which is something we observe]

If we could give the photon a mass (happens in superconductors), then a photon could be brought to rest. A photon can be linearly or circularly polarized. It can’t be polarized along its direction of travel. If you can bring one to rest, then you would have to have 3 directions of polarization. The number of degrees of freedom of our massive photon would not change. We would now have 3 directions of polarization + Higgs field.