Physics Notes: String Theory

Lecture 1: Sep 20, 2010 Back to PHY32

Topics: History, Hadrons, Infinite Momentum Frame, String Hamiltonian

Some Books of interest

A First Course in String Theory, Barton Zwiebach

The Little Book of Strings, Steve Gubser

The Shape of Inner Space , Shing-Tung Yau

Lecture Start

String Theory contains both quantum mechanics and gravity. It may well be the only theory that does.

The equations of string theory are unique, but the number of solutions is enormous.

So far, the equations are useful for reasoning about questions like – what is the entropy of a black hole?

Q: Why can’t QFT model gravity?

Originally the problem was divergences in Feynman diagrams. Now this is not seen as a fundamental problem. However, QFT with gravity does lead to contradictions in the context of black holes. For example, it predicts that black holes have infinite entropy.

The Beginnings of String Theory

In experiments hadrons were observed to occur in sequences that corresponded to steps in angular momentum. For mesons (integer spins) these graphs looked like:

The odd thing about these plots was that the mass squared was the bottom axis and that the particle sequence formed a straight line.

[If you assume that the particle structure is two quarks of equal mass on the end of a string with the extra mass, then you can figure out how much the string is stretching and how much the tension must be. If the string has significant mass, then the tension in the middle would be less and the line would not quite be straight].

Protons and neutrons have half integer spins so the steps start at spin ½ but otherwise have the same characteristic straight line on a Regge plot.

On the other hand electrons on the other hand can’t be spun up. We don’t know their size but we can put an upper bound on it. To spin one up would add too much energy.

[Unfortunately I didn’t record Prof Susskind’s analysis here, I did my own …

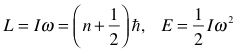
for some effective radius (the radius of gyration)

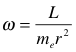
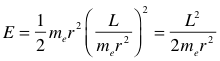
If L goes from ½ to 3/2 which is a factor of 3 increase in L, then energy associated with the spin would go up by 9. This doesn’t agree with Prof Susskind’s analysis, so I have to figure out why.

One thing that is true is that grows with the inverse square of r. The velocity of rotation is so the velocity goes as the inverse of r. For sufficiently small r this velocity reaches c which will require a different treatment.

]

Pion Scattering

Another experimental result led to modeling of strings – Pion scattering.

The Feynman diagrams involving intermediate mesons looked like:

If the process on the left exists, then the process on the right must also exist. [ It is just a time-space swap of the graph on the left.] is any of the series in the Regge plot.

If you add up all the contributions of both graphs, you get double the result of experiment. This led to new diagrams that looked like:

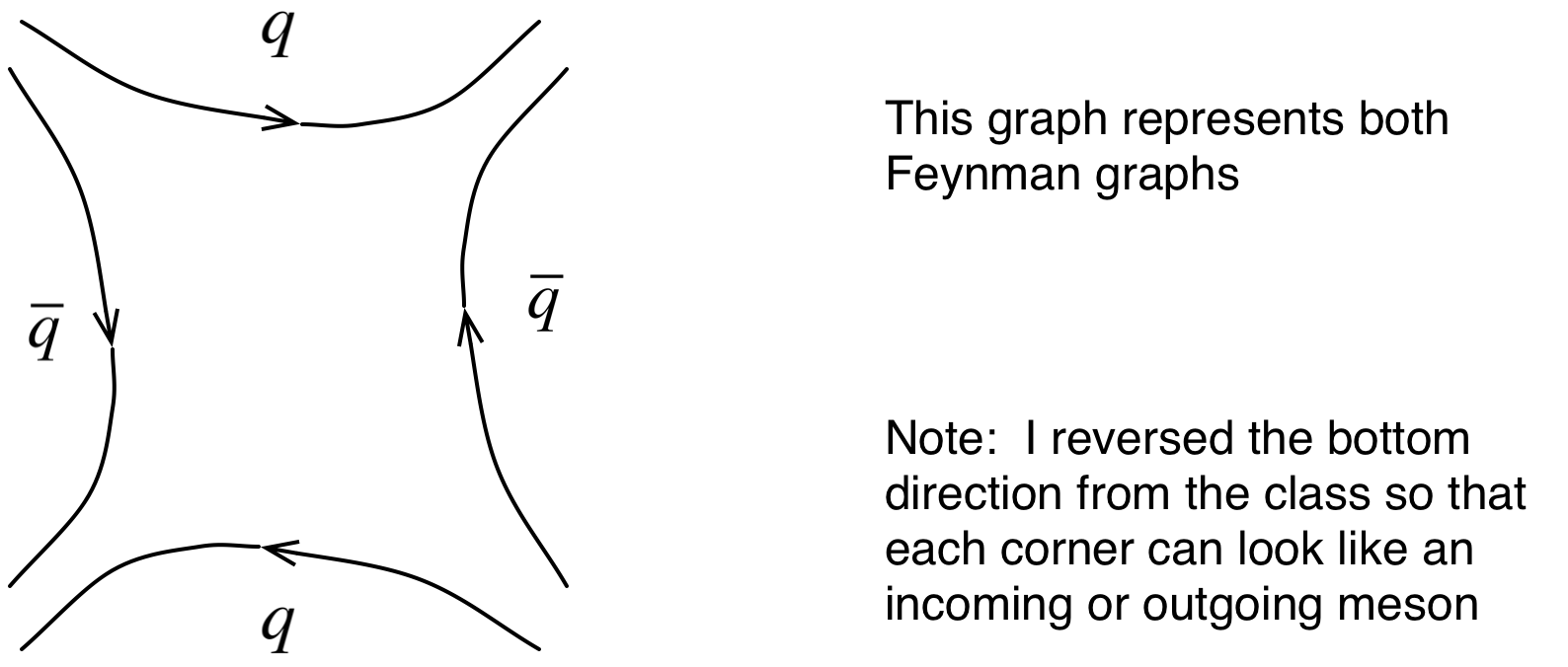
A topological interpretation is that if you cut this “sheet” model at a fixed time, then you get the graph A. If you cut it across space, then you get the graph B.

This was the origin.

If quarks are participating in this sheet, then perhaps something is holding them together (gluons). If so, then a Hadron like a meson would look like:

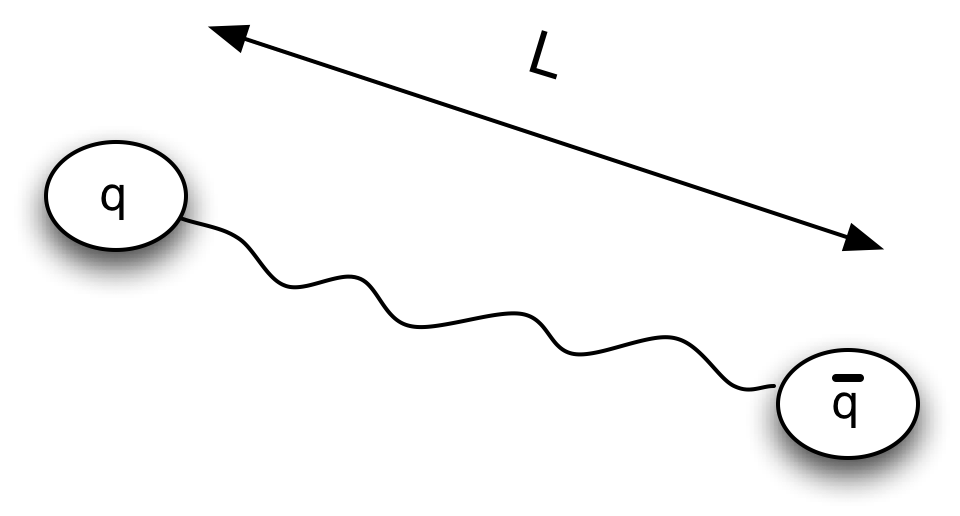
Now the meson has structure and can be spun.

You can reverse engineer the energy in the string from the Regge plots which relate angular momentum to the square of the mass. The changes in the mass are the above energy expression.

It turns out that gluon fields collapse to tubes because they are self interacting. [discussed in prior classes – find link]. As you stretch them, more and more gluons appear, adding to the energy. [suggests energy linear in length of tube]

This is all at relatively large length scales. It is an accident that string theory describes this and fundamental particles too.

This string model was promising, but never quite worked for Hadrons. The models kept generating 0 mass spin 2 particles [also known as gravitrons]. Originally this was seen as a problem in the Hadron context, but eventually became a real positive in String Theory.

Terminology: In the pion scattering diagram the area inside the quark trajectories is known as a “world sheet”. A cut across the world sheet is a string. An angled cut is just a Lorenz transform and is also a string.

Non Relativistic vs. Relativistic Physics

On the face of it, these two models are quite different. Relativistic models are correct, but more difficult.

In non-relativistic physics the energy of a particle is:

Where B is a kind of binding energy of the particle

In relativistic physics the energy is:

At low speeds with we have

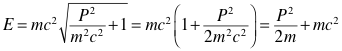
Which has the same form as the non-relativistic energy with taking the role of the binding energy.

So non-relativistic physics works well when everything is moving slowly.

The Infinite Momentum Frame (or the light cone frame)

Suppose that we have a huge positive boost along the Z axis for a collection of particles.

(dropping factors of c)

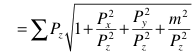
And using the same approximation for the square root as last time:

Now the sum of over our particles is a large conserved quantity. Constants offsets to energy don’t affect the Lagrangian, so we can drop the first term.

Another name for E is H, the Hamiltonian. The Hamiltonian is also the time evolution operator.

Since our energy is divided by hugely boosted values for each particle, the rate of change is greatly reduced. Another name for this is time dialation.

If we rescale H, then momentum along the Z axis is reducing the rate of change along other axes. It is in fact acting like a mass term.

takes the role of the binding energy.

Motion perpendicular to the boost direction is now non-relativistic.

Now … String Theory is expressed in the infinite momentum frame (also known as the light cone frame).

The Hamiltonian of a String

We will first model as a collection of points and then take the limit as the distance between the points goes to 0 and the number of points goes to infinity. All points are assumed to have the same mass.

where M is the mass of whole string

The spring constant between points increases with n (a chain of n springs of spring constant k has overall spring constant k/n).

The energy terms – kinetic and potential are:

Now lets parameterize the positions along the string with a variable and take our expressions to integral form:

and spring constant for unit length

is the string constant for the infinitesimal spring.

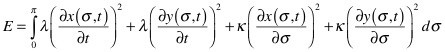
Thinking of the whole string as an object, the internal energy of vibration corresponds to the binding energy and the overall motion gives the kinetic energy of the object.

For a string at rest the internal energy is proportional to . Internal energy increases come in units of . This is true if you spin the string.

[Question to ask: Are there modes you can store energy in that do not correspond to spin? If I start a transverse or compression wave train down a string, what happens when it hits the end? Do I get a return wave train? Are the energes of these modes quantized in the same levels as spin energy, or are they much higher?]

In the boost frame the energy in the string is proportional to its stretch squared, in the rest frame the energy is proportional to the amount of stretch, as required.

Summary

Hadron experiments lead to models of strings whose energy was proportional to their length. In the infinite momentum frame this is equivalent to a classical spring model.

Other Occurrences of Strings

If you trap magnetic flux in a superconductor then it will be squeezed into a thin tube. One could do this by making a very thin hole through a conductor and passing a bar magnet through it. Then you cool the conductor until it becomes a superconductor and remove the magnet. The superconductor will exclude the field and a field loop will be trapped, passing through the small hole.