Physics Notes: String
Theory
Lecture 2: Sep 27, 2010 Back to PHY32
Topics: Preliminary Math and Physics Concepts, Model of Open String
Q: What is special about spin 2 particles?
They form a tensor field. [I take it that the connection is that gravity is a tensor field].
Q: Does String Theory still have the Higgs Boson?
String theory is more like the general theory of mechanics. You can use it to describe all kinds of things. It happens to be a framework where gravity is natural. A small number of string theories have things like the standard model. An even smaller number include something like the Higgs field.
Lecture Start
Conversion from Sums to Integrals
Suppose we have a function on the input domain 
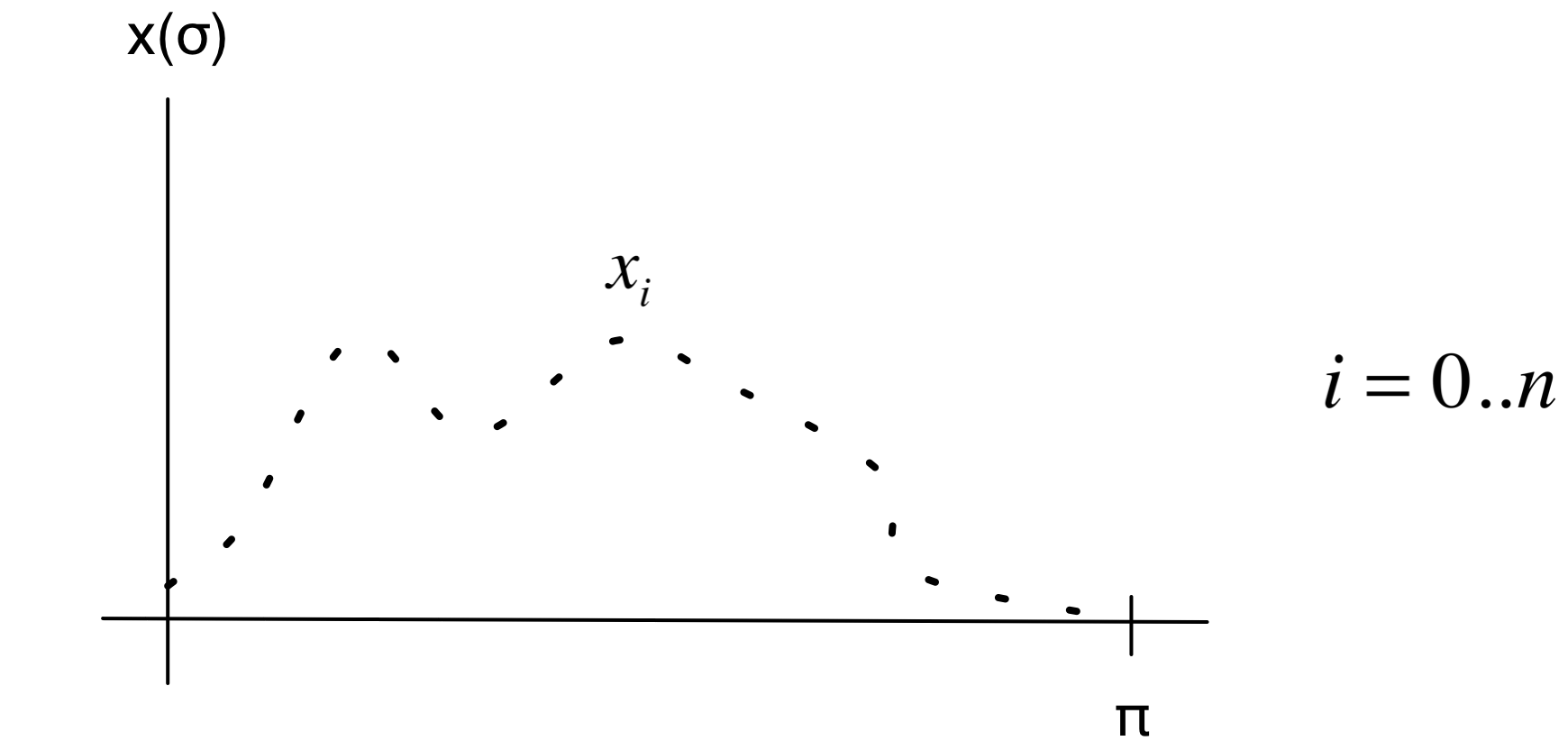
The difference between adjacent values of x is:
In the limit as we increase the number of points this difference approaches:
Also, as the number of points increases the sum converges to an integral:
Fourier Series and Boundary Conditions
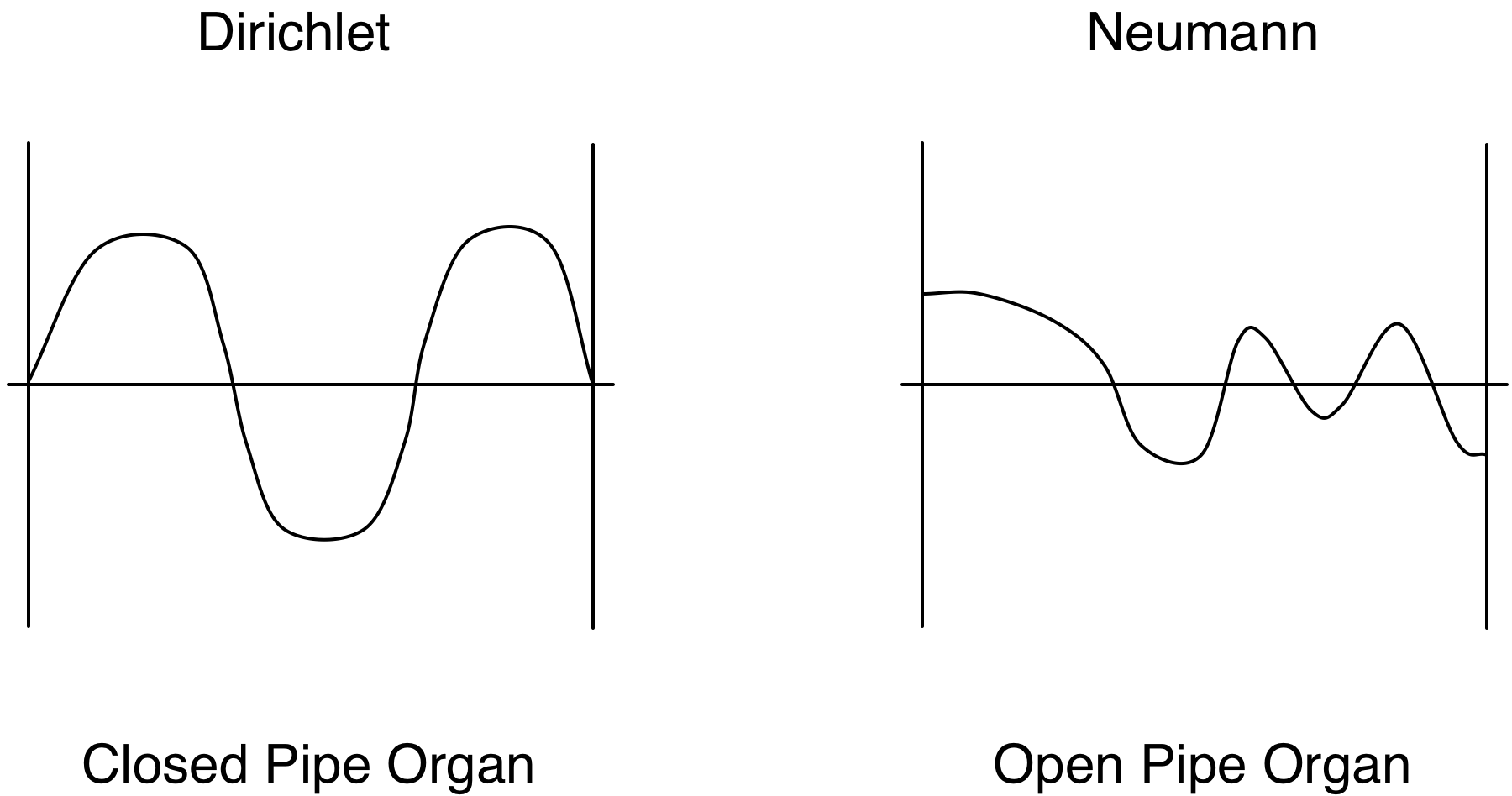
When we solve differential equations we usually have boundary conditions. In the case of a violin string the boundary conditions are obvious – the displacement at the end must be 0. There is another common boundary condition where the derivative of the displacement with respect to position is 0.
These two types of boundary conditions are named after a French mathematician named Dirichlet and a German mathematician named Neumann respectively.
Suppose we express a function as a Fourier series:
For
Dirichlet boundary conditions
For
Neumann boundary conditions
In the first case 
as required, the cos terms would violate
the boundary conditions.
In the second case the derivatives are 0 as required.
We also need to be able to determine the 
values. On the range 0 to pi, the cos() functions are
orthogonal.
This allows us to compute the coefficients as:
and
Harmonic Oscillator Facts
HookeÕs law oscillator:
(divide through by mass –
doesnÕt change physics)
This has solutions with energy
The energy levels are well separated.
What does a physicist mean by a ÒparticleÓ?
Take a cup of coffee. It has mass and position. The position is a bit fuzzy, but particles donÕt have precise locations. Why is this not a particle?
A physicist will look at the energy/mass spectrum. An electron has a unique mass with no excited states seen. If you shake the cup of coffee you can add a very tiny amount of heat energy to the molecules of the coffee. The energy spectrum is continuous.
The essential point is that a particle has a discrete energy spectrum.
For strings, the excitations are on the order of the Planck mass [which would explain why we havenÕt seen an excited state of the electron].
Review of infinite momentum frame skipped. See previous notes.
Open String Model
Let the total mass = 1. Then a model for a string with n mass points is
(include y too)
with
and 
(convention minimizes 
)
In integral form:
(
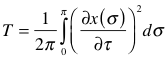is proper time)
We can recognize the Lagrangian as having a wave equation for the equations of motion. Waves travel back and forth along the string. When a wave hits the end of the string it bounces. For Dirichlet boundary conditions the wave flips on reflection and for Neumann boundary conditions it just reflects.
What boundary conditions do we have? In the middle of the string the equation of motion for a point would have both left and right terms in the potential energy. The end is special because there is only a connection to the left. The equation of motion for the last point is:
Reorganizing:
Assuming that there is a slope at the end, the acceleration of the last point goes to infinity as n is taken to infinity. This wonÕt do, so:
Conclusion: We use Neumann boundary conditions for open strings.
Energy Levels For Strings
Using a separation of variables approach we make the 
and 
functions
of proper time.
We can now substitute into the Lagrangian.
and
The kinetic energy term is
The cross terms in the product will result in 0, so this reduces to
Splitting out the n=0 case because the integral is different in that case
The potential energy term is
Something important here is that the harmonics are not coupled in the kinetic or potential energy terms. This means that each harmonic is independent.
The frequency of the nth harmonic is simply 
.
We can mostly ignore the 
terms
since they describe the center of mass motion of the strings. The internal motion/energy is in other
terms. Each oscillator
has itÕs own Lagrangian:
With energies
where
q is the number of quanta in the oscillator
We can make a table of excitations to see what energy levels and degeneracies (number of ways to get the same energy) we get:
|
a1+ |
b1+ |
a2+ |
b2+ |
a3+ |
b3+ |
a4+ |
b4+ |
energy |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
|
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
2 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
2 |
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
|
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
|
1 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
|
0 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
3 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
3 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
3 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
3 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
3 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
3 |
|
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
|
3 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
|
2 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
|
1 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
|
0 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
|
2 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
4 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
4 |
|
0 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
4 |
|
0 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
4 |
|
2 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
4 |
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
4 |
|
0 |
2 |
0 |
1 |
0 |
0 |
0 |
0 |
4 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
4 |
|
0 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
4 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
4 |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
4 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
4 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
4 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
4 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
4 |
The counts are:
E1: 2
E2: 5
E3: 10
E4: 20
E5: 36
E6: 65
E7: 110
E8: 185
E9: 300
E10: 481
E11: 752
E12: 1165
E13: 1770
E14: 2665
E15: 3956
E16: 5822
E17: 8470
E18: 12230
E19: 17490
E20: 24842
[I assume that the counts are important for thermodynamics of strings.]
The topic next session will be closed strings. Note that if you have open strings, then if the ends come near each other, then they can join forming a closed string. If you thing about strings connecting quark/anti-quark pairs, if the right ends come together, they would annihilate, joining the strings. You can have string theories with only closed strings, but if you have open strings you also have to have closed strings.
Open strings behave like photons, closed strings like gravitons.