Physics Notes: String Theory

Lecture 3: Oct 4, 2010 Back to PHY32

Topics: harmonic oscillator review, spin of massless particles including gravitons, the low lying spectrum of strings, the problem of tachyon, basics of string interaction

Lecture Start

Review of the Quantum Harmonic Oscillator as Applied to Strings

We will use the algebraic or “ladder” method.

The independent string modes have a Hamiltonian and a Lagrangian:

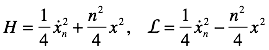
The momentum conjugate to x_n is:

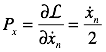
Substituting into the Hamiltonian we have

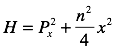
Before we think of x and P as operators, we factor (knowing that there will be a commutation error):

Scaled appropriately, the terms on the right will be the lowering and raising operators. Expanding the product out while treating P and x properly as operators.

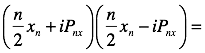
Remembering that and that we have set

The other way around yields:

Yielding a commutator:

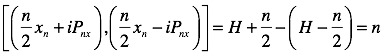
We want

instead of n, so we have to scale our operators:

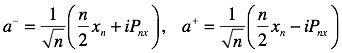
The frequency of the string oscillations is just n and all you have to do is apply a^- and a⁺ to decrement and increment the number of quanta in mode n. Each mode n will need its own raising and lowering operators which we will indicate with a subscript.

Also – we have x and y directions that the oscillations can take place in (eventually more directions), so we will need operators for each directions. For now we will use a for the x direction and b for the y direction.

String theory doesn’t work well in 2 dimensions. String theory is in 26 dimensions because we run out of letters past there :-)

Another useful thing to do with a^- and a⁺ is to solve for x and p:

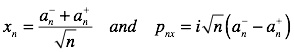
This allows us to express the string behavior in terms of these operators:

The Spin of Massive and Massless Particles

When we say a particle has spin J we mean that it has a maximum spin J. For spin J there are 2J+1 possible states ranging from –J to J in integer steps.

A massive particle has to have intermediate value of S_z. You can simply move into its rest frame and rotate the coordinate system. If you measured the particle as having spin J and then rotated the z-axis onto the x-axis, then S_z would measure a 0. So massive particles have intermediate spin values.

You can’t move into the rest frame of a massless particle that always moves with velocity c. If you have a massless particle with spin J, then by reflection symmetry you also have spin –J. There is no reason to have spin values in between and we don’t see them.

All photons are polarized. If you measure their spin, you get spin +1 or -1, never 0. A linearly polarized photon is a linear combination of left and right handed spin states. You can use the linear states or the circular states as basis states.

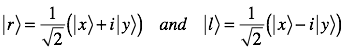
Like photons, gravitrons have only 2 states. They are often treated mathematically like two photons stuck together with the cross states outlawed. All that characterizes photons and gravitrons is momentum, energy, spin, polarization.

The Low Lying Spectrum of Strings

In the infinite momentum frame the energies correspond to m².

There is a lowest energy state where:

(also true for b)

Suppose that the ground state has energy . (In a normal quantum harmonic oscillator it would be ).

The first excitation would be:

with energy (units still a mystery)

Note: the a’s and b’s behave like polarization components. They can be summed and rotated like vectors.

Circularly polarized raising operator:

raises the ground state energy one unit

[Maybe we should really be writing this as

]

These first excitation objects are behaving as photon like objects.

[Actually, I am a bit confused here. I get that the state of the first excitation has a polarization just like a photon. However, unlike a photon there is no Z direction to move in. Perhaps the only way to make this all consistent is in the limit where the string is moving at along z.]

If they are photon like objects, then their internal energy must be 0 and:

But this leads to the intolerable requirement that

This leads to tachyons, which are bad.

Some history of tachyons

With relativity, velocity is a simple function of momentum and total energy:

if , then .

What is wrong with this? The answer is that the vacuum is unstable.

Take the wave equation

To add a mass term [see last couple of quarter’s notes] we can just add a potential term based directly on the field.

Which has a potential energy term that climbs with the field strength. In the case of a tachyon with we get:

And now the potential energy term is an upside down parabola. Any disturbance will lead to the field increasing without bound. The effect of this disturbance will then propagate at the speed of light, so tachyons don’t actually result in propagation of information faster than light.

There is also no ground state – generally a bad thing.

We need to rescue the string theory from this fate. The answer is “Super” string theory. [I assume the super has something to do with super-symmetry] We will come to this, but for now lets assume that we can eliminate the tachyons from the theory.

Originally, when string theory was being applied to hadron physics, there was an unsuccessful effort to also eliminate the photons. Later, the photon like behavior became an asset instead of a problem.

Interaction of Strings

The basic interaction mode of strings is for endpoints to join (or break apart). There is a generally a single coupling constant for this to occur should the endpoints be at the same location. This coupling constant is independent of the state of the string, but obviously a faster moving string would be near another string for less time, so the state of strings does affect interaction.

Anything that can happen can be reversed (strings can break)

Strings may just pass through each other.

A string can join itself, creating a closed loop

Any string can absorb or emit a closed loop.

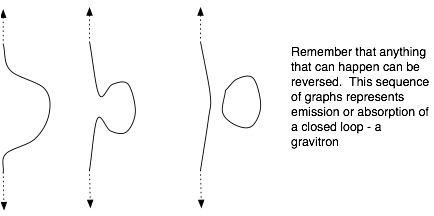
The fact that all strings interact with closed loops in a consistent way is important since we expect all strings to gravitate.