Physics Notes: String Theory

Lecture 4: Oct 11, 2010 Back to PHY32

Topics: Charge quantization (Kaluza-Klein/Dirac Monopole arguments), review of Noether’s theorem, closed string model, level matching and spin 2 state

Q: Why is charge quantized?

A: Another question is why does the proton have exactly the opposite charge of an electron? [I suppose another variant of this is why does a muon have the same charge. One might expect charge renormalization to yield different values even if the basic coupling constant was the same given that the mass of the particle is different. ]

If the charges of protons and electrons were not exactly balanced, then the universe would not be stable.

There are several arguments for charge quantization, all of which are believed to be true.

One is the Kaluza-Klein theory, which unifies electromagnetism with gravity. Apparently Kaluza noticed that if you add a 5 dimension to general relativity that you get some new field behavior that matches electromagnetism.

The unmodified field equation is:

The left hand side represents the geometric curvature of space-time and the right hand side contains the sources of gravity – energy and momentum moving in time and space directions. These are 4x4 tensors. The left hand side change for a 5^th dimension is obvious. On the right T is extended as:

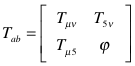where a, b range from 1 to 5

It turns out that you can identify, up to a scale factor with

For more on this see: http://www.vttoth.com/kaluza.htm

We are still missing charge quantization, which was contributed by Klein. They way he did this was to make the 5 dimension a small periodic (compact) dimension. Waves in the 5^th dimension would have their wavelength and P₅ momentum quantized by the boundary condition of periodicity. They could travel either direction, yielding opposite charges. [The consistent size of the compact dimension yields a consistent charge.]

Dirac also made an argument that if a single monopole exists anywhere, then charge must be quantized. He also came up with the idea of a Dirac string, which is a pair of magnetic poles connect by a very thin flux tube. At each end the field would look like the field of a monopole except for the direction of the flux tube.

If you set up a double slit experiment for electrons and place a monopole in the area between the slits, then electrons passing through the left and right will undergo a differential phase shift as they pass the monopole on different sides. This is related to the Aharonov-Bhom solenoid effect where an electron passing around a long solenoid undergoes a phase shift despite the fact that the electric and magnetic fields outside the solenoid are both 0. The right amount of flux (one unit) from the monopole results in the disappearance of the interference fringes. This leads to a relationship between the unit of magnetic flux and the unit of electric flux.

So if e is small then q_b must be large and the associated energy and mass would be very high.

While many physicists expect monopoles to exit, we don’t expect to find them at accessible energies.

Lecture Start

Review of Noether’s Theorem

[Continuous symmetries imply conserved quantities]

Given a Lagrangian:

with associated conjugate momentum

Suppose you have a continuous symmetry of the Lagrangian generated by:

Basically we move a small distance in a direction determined by the current q’s and we know that the Lagrangian is unchanged by a small shift in this direction.

An example is a rotation symmetry where

To rotate large angles one repeats the shift over and over.

In quantum mechanics symmetries such as spherical symmetries are characterized by a number of generators each one of which specifies a direction along which a small move does not change the Lagrangian.

Associated with each generator of such symmetries is a conserved quantity.

Closed Strings

We will parameterize closed string in much the same way as open strings. The one difference is that we will let range from 0 to .

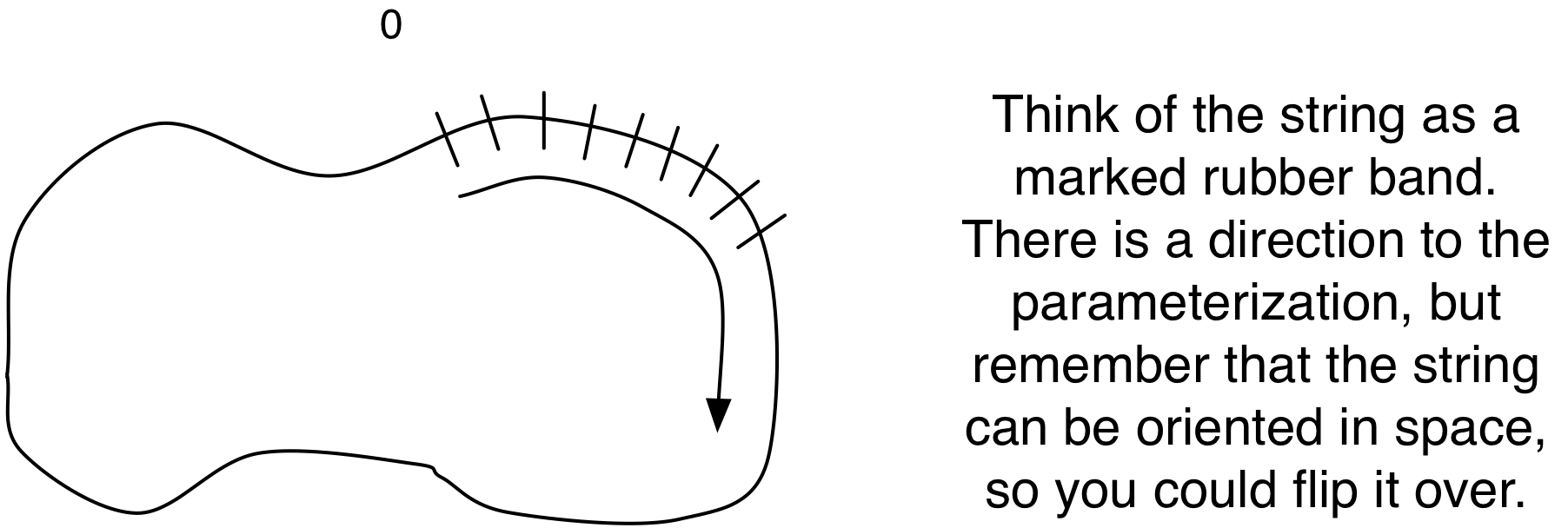
Another way to think about it is that if the string were to break, the ends would be distinguishable, much as the strings associated with mesons would have distinguishable ends. In that case one end would be a quark and the other would be an anti-quark. In this sense, the string has an internal direction in its parameterization variable , not to be confused with directions in space.

Like open strings, there are waves on closed strings. The boundary conditions are different. Instead of requiring a 0 derivative at the ends, we simply require that

We can have waves (wave packets) moving right or left along the string.

For open strings we used sin and cos functions for the Fourier series expansions for x and y. This was convenient because the boundary conditions eliminated the sin terms. This won’t happen for closed string boundary conditions, so it is simpler to use exponential terms.

Remember that:

We can express x (and y) as:

where n ranges over all integers

We can split this into three parts:

The last term is the center of mass motion of the string. The first sum describes waves moving left (negative direction) and the second describes waves moving right.

The Lagrangian for a closed string is the same as for an open string – we are just changing the boundary conditions.

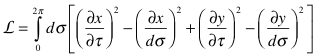
In our Fourier expansion for x and y each x_n and y_n represents a degree of freedom, each of which behaves as a harmonic oscillator with a different frequency.

We can write the energy of the string in a slightly different way that will need later:

Leaving out y for now

If you multiply the squares out and add, the cross terms in each product will cancel with each other.

The first term represents the energy for left moving waves and the second term the energy for right moving waves.

Each can be excited by the operators . What kind of states can the closed string have?

generate the 4 states from the |0> state

Linear combinations of these states are also valid. Again the combinations behave like photon polarization. These states are forced to be massless again as in the open string case.

The next increment of energy would have 14 combinations, either a pair of n=1 operators (ignoring ordering) or a single n=2 operator. Prof Susskind described the result for this energy level as garbage. [I’m not sure why this should be obvious. At the time he said it I thought I understood why, but I’ve lost it. Maybe it is just the rule below]

Some of the combinations of operators are forbidden. There is a rule called the “level matching” rule, which requires that the left and right moving energy must be the same. We will derive this from Noether’s theorem in a bit. For now we can see what the consequence of the rule is. The following is a table of operator combinations applied to |0> and whether they satisfy the level matching rule.

	Bad
	Bad
	Bad
	Ok
	Ok
	Ok
	Ok

4 of the 14 combinations satisfy the rule.

An alternative would have been to use the circular polarization base states:

Then the 4 combinations that survive the level matching rule would be:

a) L=+2

b) L=0

c) L=0

d) L=-2

I have indicated the associated angular momentum of these lowest level excitations of the closed string (remember that single operator excitations fail the level matching rule too).

The spin 2 states must be massless again.

The spin 0 states have names. One is called the axion and the other the diliton.

Why is Level Matching Required?

This is an application of Noether’s theorem. Let’s go back to treating the string as a sequence of mass points. There is no special point in the string that has to be index 1. Rotating the labels of the point will make no difference to the wave function [There is no difference when the wave function is integrated across the range. I think the following sequence involving the wave function should all be under an integral from 0 to 2 pi] or the Lagrangian.

In continuous form this translation symmetry is generated by:

and therefore:

Reorganizing:

Dividing by we get something that in the limit is a derivative:

Applying the chain rule we have [I’m sticking the integral in now]:

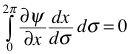
Now we need to remember the definition of momentum:

In this case q is x

This gives us the form for a conserved quantify from Noether’s theorem:

(looks like continuous version of )

[I see the match with the form of Noether’s theorem, but we didn’t really use it here. We directly showed that the integral was a constant 0.]

Now the masses are the same for all the points so we can divide the mass out of the momentums. This leaves velocity behind.

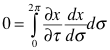
We can use this fact with the energy of a closed string. The expression was:

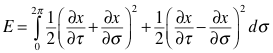(plus y terms)

Remember that we separated the energy of left moving waves from the energy of right moving waves to the left and right hand sides of this expression. If you multiply out the squares you will find that the only difference between them is the cross terms. We have just shown that these cross terms are 0. This means that the energy of left moving waves must match the energy of right moving waves.

This requirement is the level-matching rule.

Q: Is there any evidence that strings are fundamental. Could strings in turn be made of something else?

In the end, we regard an object as fundamental if it is useful to do so. Prof Susskind attributed this viewpoint to D’Hooft In the case of the electron monopole pair it is useful to think of the electron as fundamental because it has a small coupling constant and calculations converge. If the electron coupling constant e increased enough, then the monopole coupling constant would shrink and we would treat the monopole as fundamental.

Depending on string theory parameters, either strings or d-branes are “fundamental”

Next class: M theory