Physics Notes: String Theory

 

 

Lecture 6: Oct 25, 2010                                                                 Back to PHY32

Topics: Fundamental Parameters are unit-less,  adding spin to mass points, Mandelstam variables, the Veneziano amplitude,  and scattering of strings.

 

Q:   General question about parameters of the string model: string tension, mass/length É

The answer was a more general discussion of what constitutes fundamental physics parameters.   The basic answer is that the real fundamental parameters are unit-less.   Otherwise the numbers have things like the length of some kingÕs arm baked into them.

Examples of fundamental parameters:

1)   The probability that a suddenly stopped electron will emit a photon.   In general probabilities are unit-less.   This one is essentially the electric charge and is quantized.

2)   The ratio of the electron mass to the proton mass.  

3)   Values expressed in Planck units, which are set in a fundamental way.    See lecture 5.

 

String tension can be expressed in Planck units.    It would be energy/length so you would write it as a multiplier times Planck-mass/Planck-length.    Call it .   We hope for a number like 1/100 to 1/1000.   If it is too big then it will break the theory – perturbation theory wonÕt work well.         If  were small then we would see excitations and QFT wouldnÕt work.

 

Lecture Start

 

Q:  Why did the open string have a  (from past lecture)?

The first excitation had the polarization properties of a photon, so it would need to be massless.   This means it had negative energy before excitation.      [Apparently in lecture 5, which I didnÕt attend, it turns out that there is a small negative energy contribution per direction of -1/24, so you have the boost direction Z, time and 24 more to add up to -1.   Mike Peeler sent me some notes that I need to review.]

This was Bosonic string theory.     The original idea was that the individual mass points that make up a string do not have spin themselves.   A problem with this is that any combination of bosons remains a boson.    There was no way to make a fermion.      The only good thing about this theory is that it contained photon and graviton like particles.

Mass Points with Spin

Superstrings came out of trying to fix the problems.   In this case strings are made up of spin ½ mass points.  [It wasnÕt clear what the potential energy function was for neighbors – should they be like a ferromagnet or an anti-ferromagnet?   It appears slightly easier to take the continuum limit for ferromagnets, but it seems like you could just have one field variable represent the left most of each pair in an anti-ferromagnet with a second field variable for the right most of each pair and make it work anyway.  ]

Each mass point now has additional degrees of freedom associated with the spin, which can point in more directions than we are used to.

We would write the continuum form as  where ranges across the dimensions.   As you take the continuum limit, strings remain either even (boson) or odd (fermion) chain length.  

When the spectrums of chains of mass points with spin were analyzed the even and odd length strings had different spectrums.

 

 

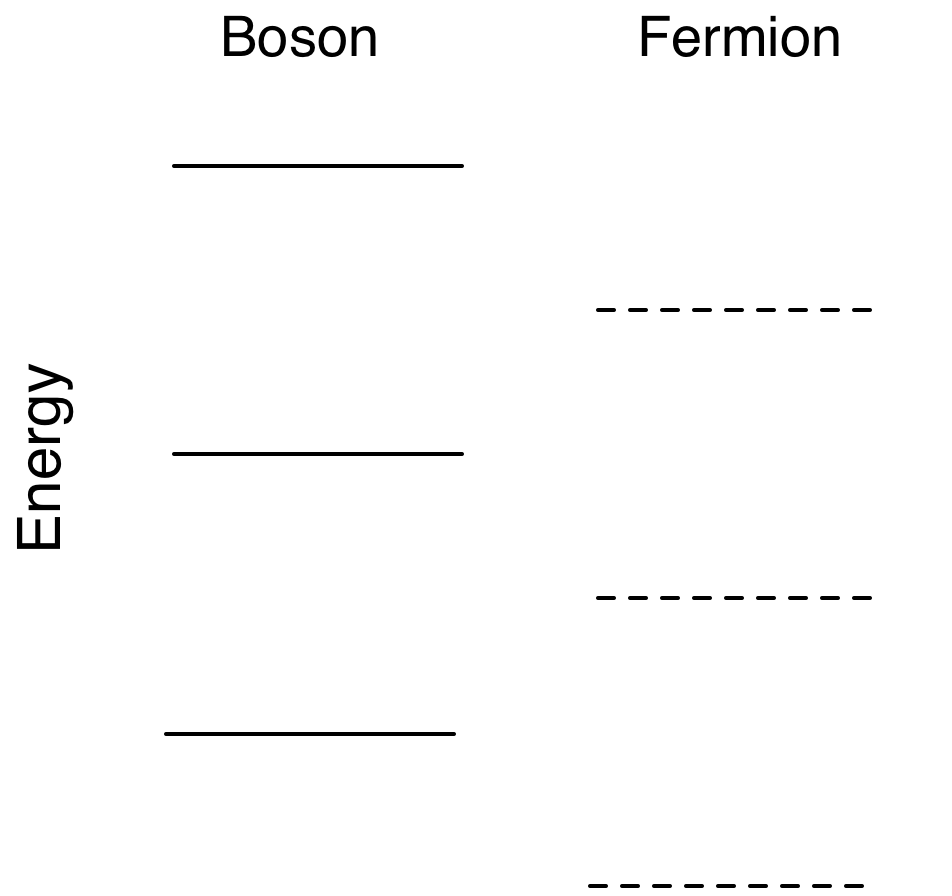
Problems Solved by including spin in mass points

1)   It solved the inclusion of fermions in the theory.   If you collide two odd strings you make an even chain,  as in .  If you break an even chain you get either two odd or two even chains.

2)   Tachyons disappear from the spectrum!

3)   Extra dimensions – the ground state has 0 mass, but leads to 10 dimensions.  The dimensions break down as 1 + 3 + 6.  One time, 3 ordinary space and 6 compact space dimensions.   Even though it sounds like the extra dimensions made some uncomfortable, they are not a real problem in the theory.

The Scattering of Strings

 

We start with the scattering of more ordinary particles.

Most of particle physics is about scattering of particles because it is about all we can do at high energies.

Suppose we have a scattering situation where we have two incoming particles, resulting in two outgoing particles.   Fundamentally we preserve the 4-momentum through the collision.

           

One scalar invariant is

           

A trick used by physicists is to treat the outgoing particles as incoming and to negate their 4-momentums.  This allows the total conservation of 4-momentum to be expressed in a symmetric way.  [There must be a better way to keep track of upper/lower indices and particle indices at the same time]

           

We have 16 parameters to deal with in this form.   First we want to simplify the problem.    We boost to a center of momentum frame and rotate the coordinate system so that the incoming particles are moving along the X-axis.    After we get our answers we can translate them back.

Note:  this only works if the particles have mass.

Now the picture of the collision looks like:

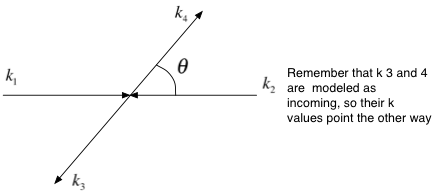
The collision we are describing is an elastic collision.

After the boost and the rotation, the parameters are describing the collision are reduced to a much smaller number.    There are a number of relativistic invariants that give us information about the outcome.

The momentum components of k1 and k2 are equal and opposite because we are in the center of momentum frame.   All that is left in a sum of k1 and k2 is the energy.

               is the center of mass energy

 

k1 + k3 describes momentum transfer between k1 and k3.   We know that the energy term on the right below must be 0 because we negated k3 and k4 and energy must be conserved.   All that is left is the momentum piece, indicated as vectors below.

           

This can be expressed in terms of the angle as:

             


[Prof Susskind didnÕt show this, but it is pretty simple –

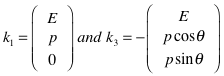                      p magnitude unchanged

So

           

                       

]

k1 + k4 describes momentum transfer between k1 and k4.   Again, we know that the energy term must be 0 because we negated the k4 term.

           

           

 Summary –   We have three relativistic invariants  which are known as the Mandelstam variables:

           

           

           

The propagators for the three Feynman diagrams that occur in the scattering process have simple forms in terms of the Mandelstam variables.   In what follows, A is the amplitude of the propagator.    g is the coupling constant for the two vertices in each of the following diagrams.

 

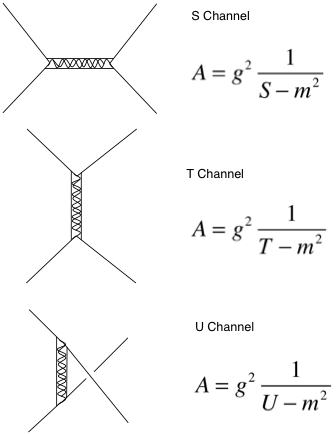
In the S channel the particles come in, form a composite that forgets the original angle and the exits are in a new angle.

In the T  and U channel the exit angle affects the amplitude.

This does not describe meson scattering well.  There are to many intermediate states, which can also be excited.

People tried to add up all the possibilities, but without success.  [I wonder if this would have been called a scattering matrix, with coupling constants to each of the possible intermediaries.   Of course the intermediaries could have intermediaries too.]

The Veneziano Amplitude

 

Gabriele Veneziano found a meson scattering amplitude formula in 1968 that described the scattering of mesons.   In this scattering formula there is no need to add up the S, T and U channels.   It seems to cover them all.

           

 

The function used here is the gamma function and is a continuous relative of factorial.

           

What kind of physics would give rise to this?  String theory

Scattering of Strings

 

We can draw a string in space as a collection of mass points moving through time.

 

 

A string moving through time traces out a world sheet.  The world sheets of two strings can collide, joining the strings.

 

 

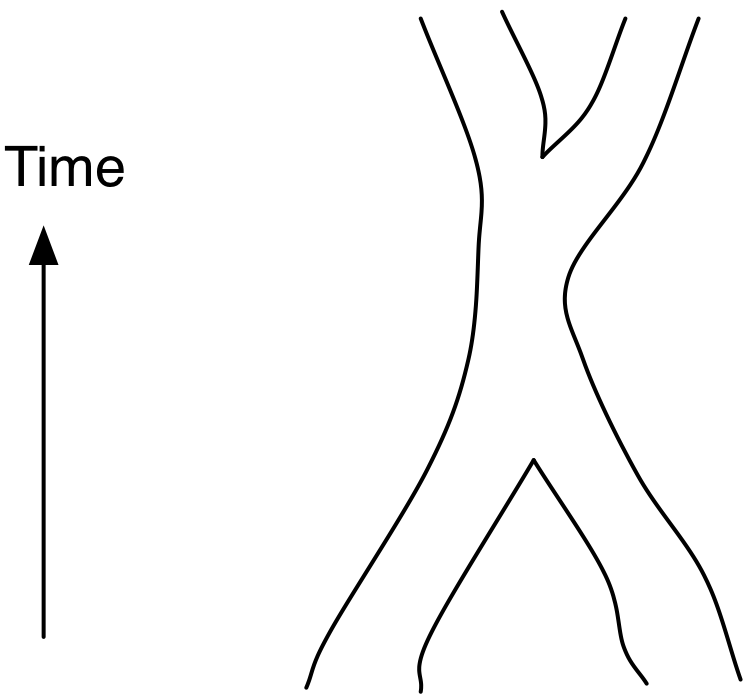
We can also show this in sigma-time space as:

 

So the idea is that the ends of the strings meet and join.   After a time , they break apart again.     To compute the amplitude we have to integrate across all ways that this can happen, so this means integrating across all time differences between the joining and breaking of the strings.

We start with the state of one string:

           

And the second string

           

 

Then at time 0 we have mass point n annihilate with mass point n+1, joining the strings.     We propagate forward in time using the Schršdinger equation [which is accurate because we are in the infinite momentum frame].   This equation relates the time derivative to spatial derivatives, which we can compute from the previously derived string states.

           

 

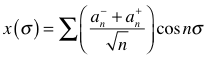
            y, z, É are similar

and

           

 

After propagating forward in time we then split the string.   The sum over all paths in space-time looks like:

           

[The middle term now looks like a standard decay term, which could correspond to the period where the string is joined.  ]

The formula does not appear symmetric.   A substitution can expose the S/T symmetry.

Let      

Then

           

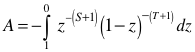
or

           

 

 

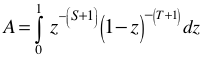
A further substitution (1 – z) = w makes the symmetry between S and T obvious.

I stuck this into Mathematica and got the result:

           

 

Which matches the Veneziano amplitude!

 

Final comment:    The scattering of photons, gravitons and scalar particles are distinctive.    The calculations based on the string model match that behavior.