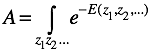Physics Notes: String Theory

Lecture 8: Nov 8, 2010 Back to PHY32

Topics: Path Integral Issues, Conformal Mapping, Scattering

Q: In the path integral formulation the integral is over all paths or surfaces. While the value being integrated is simply , it is not clear what it means to integrate over all paths. What would the “dp” in this integral be?

A: [I’m not sure of Professor Susskind’s exact words here so I’m paraphrasing: ] This is a very tricky subject, beyond what can be covered in this class, and easy to g to formulate incorrectly so that path integrals don’t converge or yield the wrong answer.

Very similar integrals came from work on random walks. These integrals are called Weiner Integrals. You can imagine a particle starting a given point making a sequence of random jumps where the probability of the jump depends on the distance. You can then ask the question, what is the probability density for the particle to arrive at a second point. If you take a limit of the number of jumps going to infinity and the expectation value of the displacements going to 0 you have a kind of integral.

These random walk integrals led to the Feynman path integral.

You can think of our strings as rubber bands in a thermal bath. Over time the rubber band sweeps out a trajectory in space-time. What is the probability that the rubber band goes from state A to state B?

This type of integral must make sense, but it leads to requirements on the dimension count to avoid divergence. This is what leads to 26, 11, or 10 dimensions depending on the string description.

When we use conformal mapping to solve problems in Electro-Magnetism there is the complication that the field is really a 2-form (a rank 2 tensor). A change in coordinates yields a change in the field components. For example, an electric field will transform into a magnetic field under boost.

In the case of string theory the coordinates of a string behave like scalars and do not change under coordinate transformations.

Lecture

Conformal mappings

For Electro static problems in 2 dimensions, what is the force law and potential function?

The force is

and the potential function

Potential is a scalar, which makes it easier to work with in many cases.

The relationship is as usual:

We also know the relationship between the electric field and charge density.

Expressing in terms of we have

or

As we have seen, this equation is unchanged by a conformal mapping of the coordinates. A bit later, we will apply the electrostatic analogy to the string scattering problem. Before we do that we need a better understanding of the space of conformal mappings in 2 dimensions (the space).

Conformal Mappings in Two Dimensions

In two dimensions we can simplify the analysis by treating the space as the complex plane.

The mappings of interest are bijections between two regions in the complex plane.

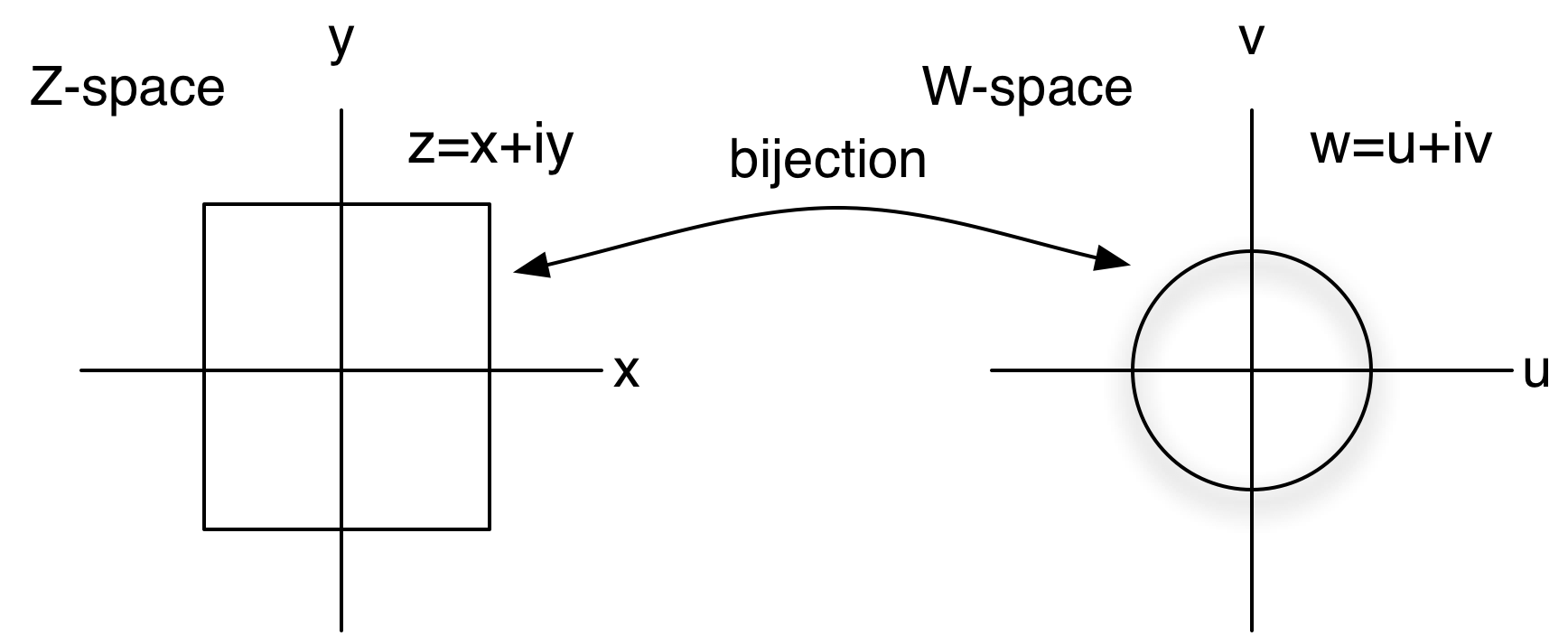
As a first step in determining which mappings are angle preserving we need to understand some properties of derivatives of complex valued functions.

We start at point that maps to point . A displacement from of yields a displacement of of .

Then we expect that.

But the direction of our displacement might matter. Lets start by insisting that displacements along x and y yield the same answer.

In general

Along the x-axis we have

Along the y-axis we have

And since we require that these be equal we have the two equations

The Cauchy-Riemann Equations

Homework: Show that requiring the derivatives to match along the x and y axes says that they match in any direction.

We can take another step and uncouple these equations taking an additional derivative

Adding these two equations and simplifying we have

Following the same process with the other derivative we also get

So the Laplace equation comes back again.

Homework: These equations imply the Cauchy-Riemann Equations. Prove this. [I’m not sure I got this right. I’ll come back and give it a go.]

Analytic = Conformal

Let’s write two small displacements from . We write them in polar form because of the direct connection to angle.

and

If we take the ratios of the two displacements we get a complex number whose angle is the difference between the original angles.

The magnitude of this ratio is not important; all we care about is the angle.

These displacement vectors also lead to corresponding displacement vectors in the W plane.

We can compute the equivalent ratio of displacements in W using the derivative at .

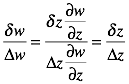
We rely on the derivative being the same in all directions. Since the ratios are the same in Z and W, the angle difference between the displacement vectors must be the same.

Example 1

So equating real and imaginary parts we have

We can now test this mapping with the Cauchy-Riemann Equations

and

So this mapping is analytic and conformal.

Example 2

This gives

Testing

So complex conjugation is not conformal.

Example 3

this gives

Testing

and

So this mapping is analytic and conformal.

Example 4

This example is important in string theory.

Where

and

We can write w as

Then

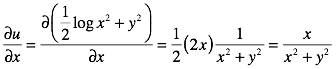
and

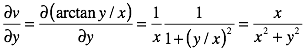
That’s one half of the Cauchy-Riemann equations, now for the second half

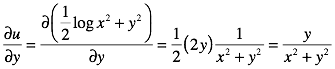
and

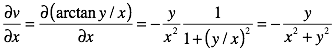
This checks out too.

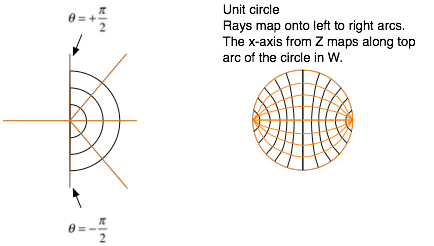
Since this case is important for string theory, lets look at how it maps the right half plane.

Circles in Z are mapped into vertical straight lines in W. Radial lines are mapped to horizontal straight lines. So the right half plane is mapped to a ribbon of width . The point a 0,0 in Z is a special point that maps to u=-Infinity on the left and since every circle, no matter how small in Z, maps to a line of length , this special point can be used to represent an incoming string.

If you map the whole plane to W you get a wider strip, but you have to identify the top edge with the bottom edge since they represent the same set of points in Z. This generates a cylinder, which is a good mapping for a closed string.

Example 5

This case is an example of linear fractional mapping. Under linear fractional mapping circles and lines are mapped to circles and lines.

The left half of the Z plane is mapped outside of the circle.

Scattering in String Theory

Scattering behavior in string theory is nearly the definition of string theory. We return to the diagram of two strings joining for a time and then breaking apart.

We integrate the action over all join times.

The momentum of the incoming and outgoing particles has to be added in (integrated over). In the original diagram the incoming and outgoing strings are at , and different ranges in . We can use conformal mapping to map the space onto the unit circle, with the injection points on the edge of the circle. This makes the integral simpler.

It turns out that under conformal mapping, we have freedom to place n-3 of the points on the edge of the circle and the remaining three points will be determined. [Something to investigate].

The rule for handling these special points is that we add a factor with fixed k.

to the integral. These factors are known as vertex operators. [It looks like the conformal mapping would have a failure – angles not preserved - at the injection points. Perhaps this is compensation for that failure]

Now we integrate over the positions of the insertions in the new space.

The good news is that these integrals can be done. They don’t converge except in the right number of dimensions.

We can think of the components as independent electrostatic fields that must separately satisfy the Laplace equation with boundary conditions. The perpendicular E field must vanish at the edge. The charges are the components of the momentum .

We can sum up the energy associated with the dimensions, giving an action expression, which is integrated over the injection points.