Physics Notes: String Theory

Lecture 9: Nov 22, 2010 Back to PHY32

Topics: Gravity and String Theory, Compactification, Energy Spectrums Associated with Compact Dimensions, T-Duality

(Random) Questions before class?

Q: What’s up with the detection of gamma rays from the areas above and below the center of our galaxy.

There are two bubble like structures extending out about 50,000 light years above and below the center. The gamma rays are the result of fast moving particles colliding with dust and gas in the space. If you assume that the particles are moving at a significant portion of the speed of light, say 10%, which makes sense given the energy of the gamma rays detected by the Fermi satellite, then the timing of the event would be on the order of 0.5 to 1 million years ago.

In such events, the first think you want to know is the total energy released. That would inclusion or exclusion of possibilities like swallowing of a star by the central black hole.

An audience member made a comment about the existence of a black hole at the center of the galaxy.

This is the movie of starts orbiting the central mass in our galaxy.  

http://www.astro.ucla.edu/~ghezgroup/gc/pictures/orbitsMovie.shtml

The key thing to look for is how tight the orbits are.  There is one star that appears to make a sudden 180-degree turn.  From the width of the orbit you can determine a limit on the volume of the mass.   From the path orbit, you can determine how massive the central object is.     Divide the mass by the volume and you get a density well above the density of a neutron star.    This is good evidence that the central object is a black hole.

Q: Why is the LHC colliding lead ions?

They are doing it to make a quark-gluon plasma where the quarks are no longer bound together in protons and neutrons (or mesons). There are theoretical calculations of the behavior of such a plasma, but this is a chance to find new physics. After a plasma is formed, there will be thousands of particles flung off in different directions and energies. From this result we can decode what happened. We want to know things like the flow properties of a quark-gluon plasma. What is its viscosity? …

The best models are based on the string theory of hadrons.

Lecture

The topic is the connection between gravity and string theory.

We start with the motion of a point particle on a curved surface.

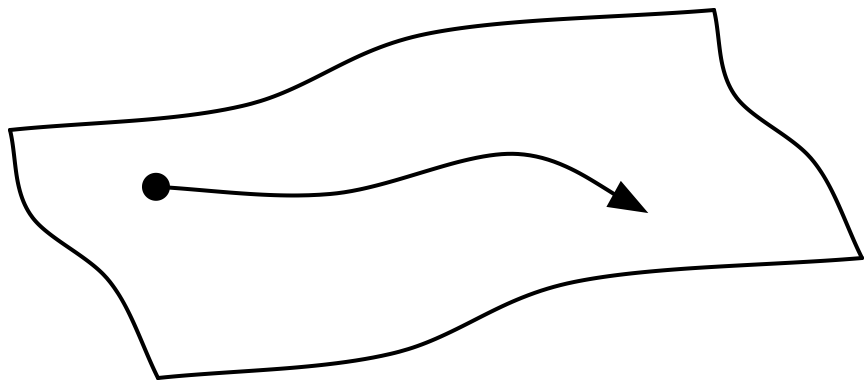
There are constraint forces holding the particle in the surface. If there are no forces in the surfaces, then the particle follows a special trajectory called a geodesic.

We can model the behavior of the particle by breaking the trajectory up into a set of discrete segments and then take a limit.

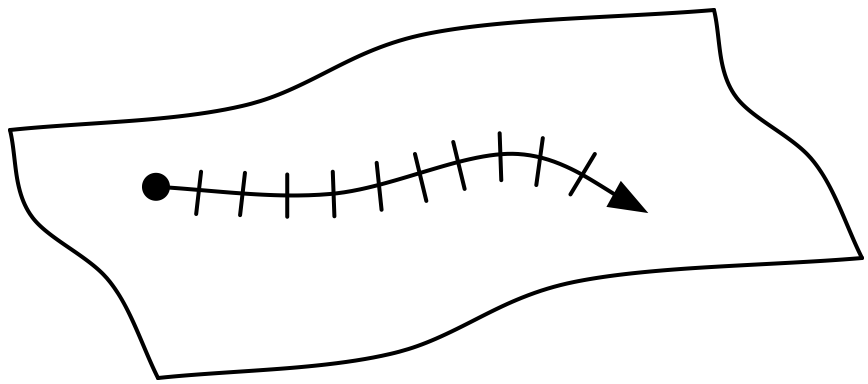
A good question – is this limit well defined? The answer is that the limit makes sense on a smooth differentiable surface.

Suppose that we generalize this limit to quantum mechanics. Now the formulation is a path integral from the starting configuration to the ending configuration. We have to sum over all paths, even wildly varying ones. This seems much more complicated and difficult to show that the limits are well defined. However, such path integrals have been shown to be equivalent to solving the Schrödinger equation. Computing path integrals is a more difficult task, but the limits do exist.

In string theory we have extended objects moving in surfaces, where a surface has fewer dimensions than the whole space. Suppose we use a sphere with radius R for the surface and model a point particle to start.

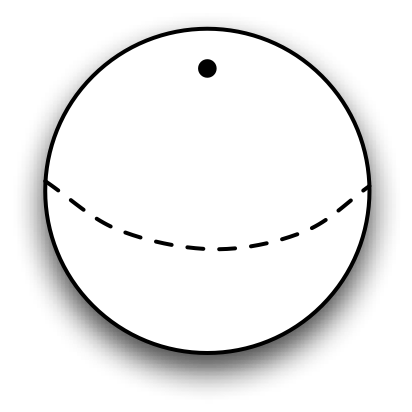
We can write a Lagrangian for the free particle.

Note that the velocity is always tangent to the surface. What path does the particle follow? It follows a geodesic known as a great circle.

We can write the Lagrangian in terms of angular momentum, which makes it easy to see that momentum is quantized.

Some basic relationships

Using these relationships we can rewrite the Lagrangian

But we know that angular momentum is quantized in units of .

Now let’s switch to a string. Now the limits don’t exist. Let’s see why.

The string has zero point oscillations, giving the string a little size.

We can use our previously derived coordinate expression to figure this out. We will use the form written in terms of the raising and lowering operators.

See lecture 3 for details.

It is easier to compute the average squared size. We only want the displacement from the center, so we drop the center position.

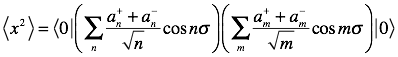
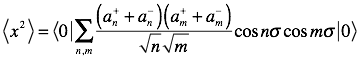
yields zero applied to the vacuum on the left and yields 0 when applied to the vacuum on the right. Only the -+ combination survives.

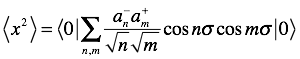
If m is not equal to n, then the operators commute, also yielding 0, so contributions come only from cases where m=n. We are left with

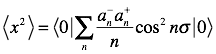
As we integrate each term the various pieces yield constants. 1/n is a constant. The operator pair reduces to 1 and the integral of cos² yields ½. Now we have a simple sum.

And we have big trouble. This is infinite.

We could try things like dropping the high frequency oscillations, but then it wouldn’t be string theory.

What we can do instead is to parameterize the average squared displacement with a cutoff value of n and take the limit later. It turns out that in flat space; this works and the high order contributions cancel out. As a function of n the average displacement squared has the form

The Lagrangian for the string on a sphere still has the form.

However, as the string grows, the moment of inertia diverges from mR².

This happens because different parts of the string are at different distances from the axis of rotation.

[I would have thought that as the string became evenly distributed across the sphere, that the moment of inertial would go to the value for a hollow sphere.

On the other hand, the metric for this space is going to cause some problems with the coordinate solution we used for the string.

There are cross terms now.

This will affect the potential energy term in the Lagrangian for the string.

I suppose that taking these details into account will justify the next statement.]

The string behaves as if it is moving on a smaller sphere. This happens because of something called a renormalization group and happens in any number of dimensions. As the effective radius goes to 0, the moment of inertia also goes to 0, making the energy infinite.

So it turns out, strings on spheres do not make sense. For strings to make sense, the effective geometry shouldn’t change (should converge) in the limit as n_max is increased. This change in effective geometry is proportional to the Ricci curvature.

[I looked this up for compact manifolds and the more detailed form is interesting.

See Ricci_flow.

Where n is the dimension of the manifold

]

The result is that we need spaces that are Ricci flat for strings to propagate sensibly.

is the vacuum field equation for gravity.

The full equation in 4 dimensional space-time is

Where the right hand side contains all the sources of the gravitational field. In a vacuum, this is 0 and we have

We can raise and contract, giving

But a contracted metric tensor just yields the number of dimensions.

Consistency requires , which is the GR equation for empty space.

We will also need to have the right number of dimensions to make spaces Ricci flat in a way that is independent of n_max , the string mode cutoff. [I think that’s what he said]

What do we do with the extra dimensions in string theories?

Let’s start with a one-dimensional world. We have a line on which we have particles that can move left and right.

Under a high-powered microscope we might see

Now the original particles are lines and we can have point particles that can move both along and around the cylinder. This creates a new degree of freedom associated with the new direction.

The small cylinder is the most elemental and simple compactification scheme.

We can apply this compactification scheme to a two dimensional world as well.

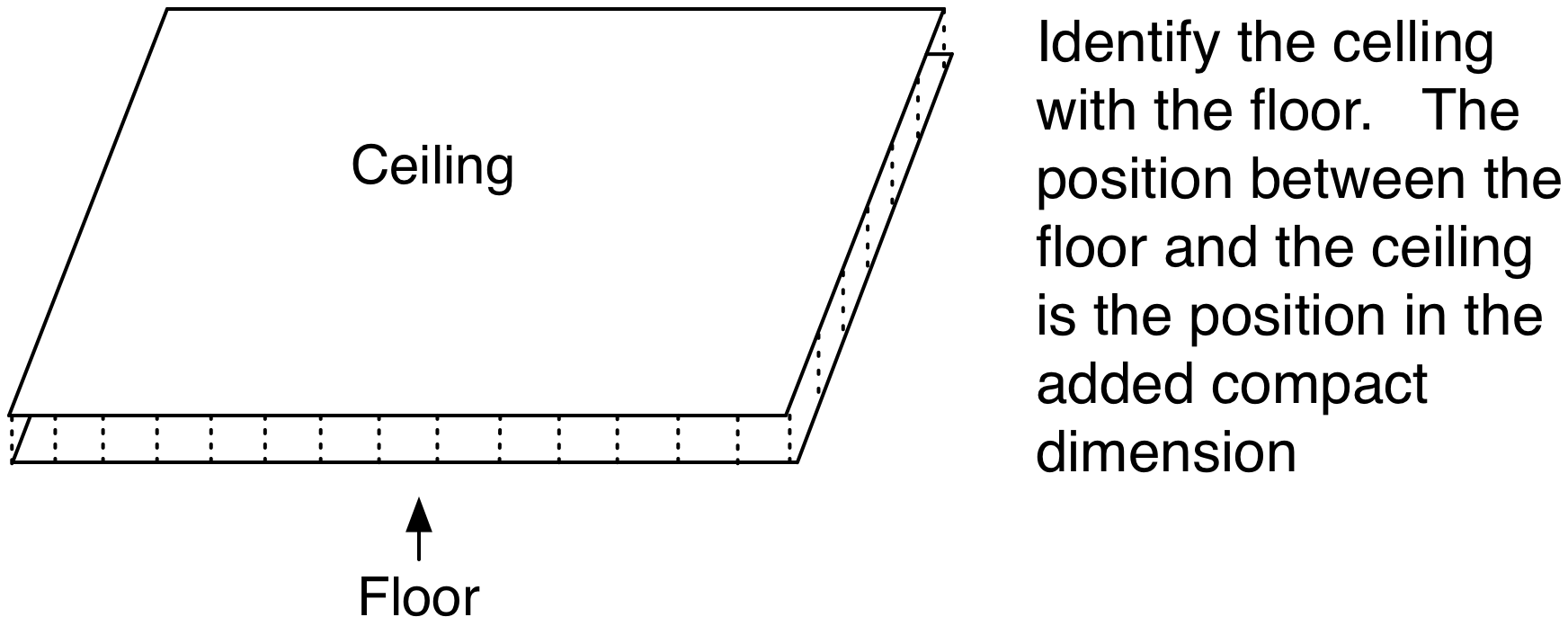
This type of dimension is known as a periodic dimension. When a path passes out through the floor, it wraps around, coming in through the ceiling in the corresponding spot.

We could compactify 2 of the 3 dimensions, leaving only one infinite one.

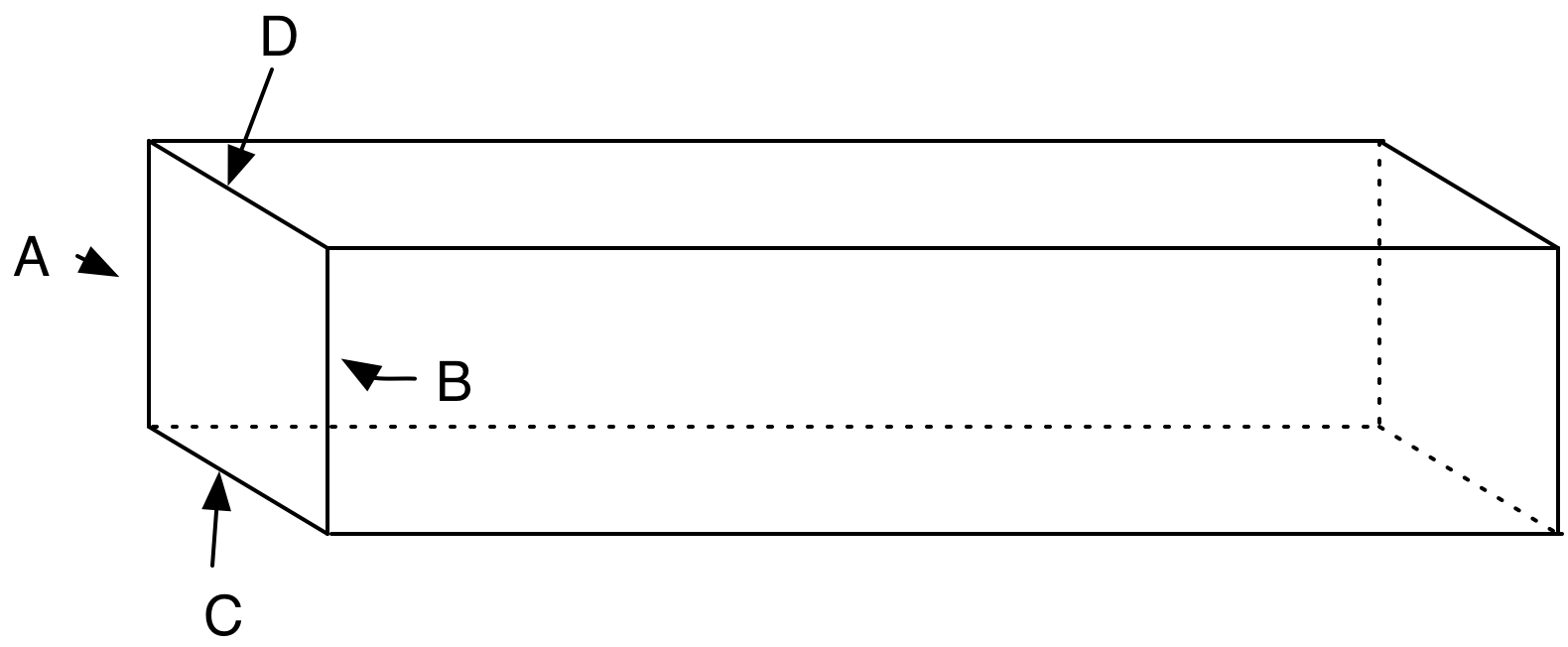
We identify edge A with edge B, then we identify edge C with edge D. This is toroidal compactification.

If one makes two slices in a stretchable bagel, then the surface can be unfolded and stretched into a flat sheet.

One could also use a line X sphere compactification, but as we saw previously, it would fail the Ricci flat requirement.

Variations on a Torus

A 2d torus can be represented as a two dimensional rectangular sheet with opposite edges identified. What freedom do we have in making different tori? We can change the aspect ratio.

We can also rotate one edge before identifying opposite edges.

The aspect ratio and the edge rotation are parameters for the Moduli Space of Tori.

There are other Ricci flat manifolds. A particularly important one in string theory is the Calabi-Yau manifold. It has much more complex symmetry properties which provides a better match with the real world.

For this class, the tori are sufficiently complex and we will stick with them.

Quantization on a Compact Manifold

On a small cylinder we can have momentum along the cylinder and around the cylinder. As previously discussed, the momentum around the cylinder, in the compact direction, is quantized.

Think of this as angular momentum

This yields a spectrum of energies for a massless particle that in our 4d world would correspond to a spectrum of rest masses. Letting we have:

Another way a string can have energy is to be wound around the dimension. This stores potential energy in the stretching of the string.

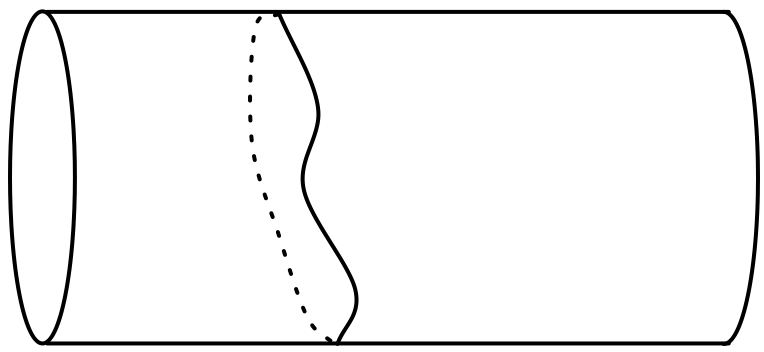
The string can be wrapped 0, 1, 2 ... times. If a string has a direction, then it can be wrapped positively or negatively, but with the same potential energy. This generates a second spectrum of energies with a step size proportional to the radius.

Depending on the size of the dimensions, these spectrums swap roles. For large r, the Kaluza-Klein particles have a fine spectrum and the wound particles have large discrete steps in energy. For small r it is the other way around. This symmetry turns out to be an exact symmetry called T-Duality.